… die du nicht selbst gefälscht hast. Bei dem Begriff „Statistik“ verspüren sicherlich einige Excel-Anwender eine leichte Gänsehaut. Offen gesagt gehört dieses Fachgebiet auch nicht gerade zu meinen Steckenpferden.
Daher kommt im heutigen Artikel wieder ein Gastautor zu Wort. Robert Grünwald wird uns alle ein wenig in die Untiefen der Statistik einführen und zeigen, wie Excel bei statistischen Fragestellungen behilflich sein kann – und wo die Grenzen des Programms liegen.
Vielen Dank an Robert für den nun folgenden Gastartikel.
Als weit verbreitetes Office-Tool stellen Tabellenkalkulationsprogramme wie Excel und seine Alternativen einen einfachen Weg dar um schnell und in begrenztem Umfang statistische Auswertungen vorzunehmen.
Dabei kann es sich sowohl um die deskriptive Aufbereitung anhand von Kennzahlen und Grafiken handeln, als auch um einfache inferenz-statistische Anwendungen.
Im folgenden Artikel möchte ich euch die typischen Beispiele für eben solche Analysen anhand einfacher Beispiele vorstellen. Dabei werden wir auch die Grenzen von Excel kennenlernen und darüber hinaus alternative Programme für eine statistische Auswertung aufgezeigt kriegen.
Deskriptive Datenanalyse – Kennzahlen
In der Statistik werden qualitative (verbalisierte) und quantitative (numerische) Merkmale unterschieden, wobei qualitative Daten in der Regel durch eine numerische Kennung codiert werden. Wird die Codierung nicht angewandt, erweist sich Excel leider als wenig nützlich, da zur Berechnung numerische Werte vorausgesetzt werden.
Erfasst man beispielsweise das Alter, so ist dies bereits ein quantitatives Merkmal, beim Geschlecht hingegen wird den Ausprägungen ‚männlich‘ und ‚weiblich‘ der Wert 1, respektive 2 zugewiesen.
Wird anstelle des Geschlechts die Zustimmung zu einer bestimmten Aussage gemessen, so spiegeln die numerischen Werte die Rangfolge wider.
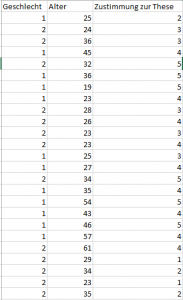
Für das folgende Beispiel werden für 25 Befragte das Alter, das Geschlecht und die Zustimmung zu der Aussage ‚Bei sonnigem Wetter fühlt es sich draußen wärmer an.‘ gemessen.
Dabei verwenden wir 1 für männlich, 2 für weiblich und tragen die Zustimmung auf einer Skala von 1 (keine Zustimmung) bis 5 (volle Zustimmung) ab.
Beispiel 1: Umfrage
Nun können für die drei Merkmale unterschiedliche Kennzahlen ermittelt werden – für das Geschlecht macht nur der Modalwert, der am häufigsten gemessene Wert, Sinn.
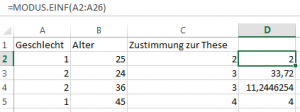
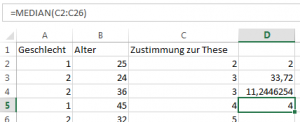
Bestimmt wird dieser entweder mittels MODUS.EINF(erste Zelle : letzte Zelle)
Modalwert berechnen
Die ausgegebene 2 bedeutet, dass mehr Frauen als Männer befragt wurden.
Für das Alter lassen sich gleich zwei Kennzahlen ermitteln – der Mittelwert und die Standardabweichung. Da diese die gemessenen Werte direkt gewichten, können sie nur für quantitative Merkmale bestimmt werden. Der direkte Aufruf erfolgt über
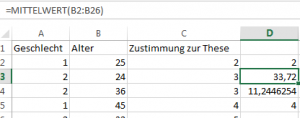
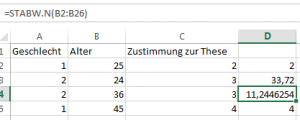
MITTELWERT(erste Zelle : letzte Zelle), bzw. über STABW.N(erste Zelle : letzte Zelle)
Mittelwert berechnen
Standardabweichung berechnen
Die Werte 33,72 und 11,34 lassen sich dazu wie folgt interpretieren – die Befragten sind im Durchschnitt 33,72 Jahre alt; etwa zwei Drittel aller Befragten sind zwischen 22 und 45 Jahren alt.
Für die Zustimmung zur These lässt sich – aufgrund der Rangordnung – der Median bestimmen.
Der Befehl dafür lautet MEDIAN(erste Zelle : letzte Zelle) und das Ergebnis ‚4‘ bedeutet, dass 50% der Befragten mindestens zustimmen, wenn nicht sogar vollkommen zustimmen.
Median berechnen
Alle Funktionen können auch über das Menü „Formeln“ ausgewählt werden; hier finden sie sich im Untermenü „Statistisch“.
Deskriptive Datenanalyse – Diagramme
Eine weitere Möglichkeit der Datenaufbereitung sind Diagramme – neben den üblichen Säulen, Balken und Torten bietet Excel hier die Möglichkeit eine Regressionsanalyse zweier quantitativer Merkmale durchzuführen.
Dabei wird zunächst für die erklärte Variable Y eine funktionale Abhängigkeit von der erklärenden Variable X angenommen, also Y=f(X). Während die statistischen Standardprogramme hier mehrere Funktionstypen unterstützen, muss in Excel mit der linearen Regressionsanalyse vorliebgenommen werden.
Die Koeffizienten der Regressionsfunktion werden nach der Methode der kleinsten Quadrate bestimmt, die Gerade kann direkt im Diagramm dargestellt werden.
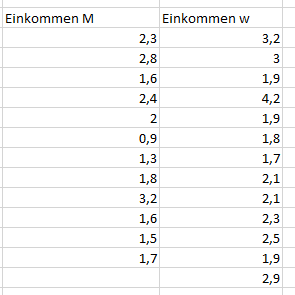
Für unser Beispiel ergänzen wir den Datensatz um das monatliche Einkommen der Befragten in T€ und wählen zunächst unter ‚Einfügen‘ das XY-Punktdiagramm aus.
Das Diagramm kann mit der Maus beliebig auf dem Datenblatt platziert werden, danach werden die
Datenreihen ‚Alter‘ und ‚Einkommen‘ ausgewählt.
Punktdiagramm erstellen
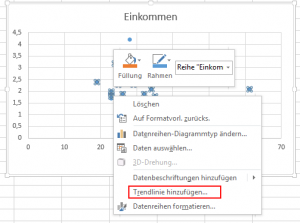
Mit einem Rechtsklick auf das Datenfeld kann nun die Trendlinie hinzugefügt und danach rechts die Option ‚Gleichung anzeigen‘ gewählt werden.
Trendlinie hinzufügen
Im Beispiel lautet die Regressionsgleichung Y=0,0029X+2,086 – dies bedeutet, dass die Befragten ein Mindesteinkommen von 2.086 € haben und dieses pro Jahr um 2,9 € steigt.
Inferenzielle Datenanalyse – Unabhängigkeit
Das neben der Datenaufbereitung wichtigste Anwendungsgebiet der Statistik liegt in inferenziellen Analysen – hierbei geht es stets um den Test der Arbeitshypothese „zwei Merkmale sind voneinander abhängig“ gegen die Negation „die betrachteten Merkmale sind unabhängig“.
Zur Entscheidungsfindung wird die zu einem vorher festgelegten Irrtumsniveau- (in der Regel 5%) Prüfgröße ermittelt. Im zweiten Schritt wird aus den Daten die Teststatistik ermittelt, anhand derer entschieden wird – liegt sie unterhalb der Prüfgröße, wird die Arbeitshypothese verworfen, liegt sie oberhalb, kann diese angenommen werden.
Unabhängig davon ob die Daten qualitativer oder quantitativer Natur sind, ist der Chi-Quadrat Test anwendbar.
Im Beispiel wird dieser auf die Merkmale ‚Geschlecht‘ und ‚Zustimmung zur These‘ angewandt.
Dazu wird zunächst die Prüfgröße mit dem Befehl
CHIQU.INV.RE(Wahrscheinlichkeit; Freiheitsgrade) ermittelt. Die Freiheitsgrade sind dabei das Produkt der möglichen Antworten weniger 1, also 1 mal 4.
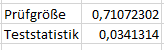
Mit CHIQU.TEST(array 1; array2) wird danach die Teststatistik ermittelt.
Da diese im Beispiel mit 0.03 deutlich unterhalb der Prüfgröße von 0.7 liegt, kann nicht angenommen werden, dass das Zustimmungsverhalten vom Geschlecht der Befragten abhängt.
Prüfgröße und Teststatistik
Inferenzielle Datenanalyse – Abweichung
Für den Fall quantitativer Merkmale, die für zwei Gruppen gemessen werden, kann mittels des t-Tests nach Student untersucht werden, ob die Arbeitshypothese ‚Die Gruppen unterscheiden sich‘ verworfen werden muss oder angenommen werden kann – maßgeblich sind auch hier die Werte der Prüfgröße und der Teststatistik.
Zunächst muss für jede Gruppe ein neues Array angelegt werden, in das die Werte kopiert werden:
Einkommensstatistik
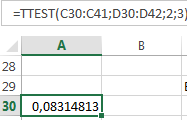
Danach kann der Befehl TTEST(array 1; array 2; Seiten; Typ) aufgerufen werden, um die Teststatistik zu ermitteln. Dabei besteht die Möglichkeit, zwischen einem einseitigen und einem zweiseitigen Test zu wählen. Der Typ gibt an, ob die Gruppen als gepaart (1), ungepaart mit gleicher Varianz (2) oder ungepaart mit unterschiedlicher Varianz (3) angesehen werden sollen.
Teststatistik
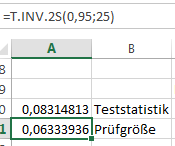
Danach wird mit T.INV(Wahrscheinlichkeit; Freiheitsgrade) die Prüfgröße bestimmt und wieder verglichen, ob die Teststatistik größer oder kleiner als die Prüfgröße ist:
Prüfgröße
Da im vorliegenden Beispiel die Teststatistik mit 0.08 größer als die Prüfgröße mit 0.06 ist, kann angenommen werden, dass sich das Einkommen männlicher und weiblicher Befragter signifikant unterscheidet.
Fazit
Aufgrund des zugänglichen Interface ist Excel hervorragend für einfache statistische Analysen geeignet, kommt jedoch schnell an seine Grenzen. So ist die Bestimmung der Kennzahlen nur für unveränderte Rohdaten möglich, für aufbereitete Häufigkeitstabellen geht dies nur über mehrere Formeln.
Bei der Regression lässt sich die Gerade grafisch darstellen und die Gleichung anzeigen, allerdings sind multiple Regressionsverfahren nicht möglich. Auch lässt sich für die Arbeitshypothese „Die Merkmale hängen linear voneinander ab“ kein Test durchführen – in R und SPSS wird dieser standardisiert mit der Ermittlung der Koeffizienten durchgeführt.
Bei den inferenziellen Methoden zeigt sich am deutlichsten, dass Excel es mit den ausgewiesenen Statistikprogrammen SPSS, STATA und R nicht aufnehmen kann – die Durchführung der Tests ist wesentlich umständlicher und lädt zu Fehlern ein. Andererseits fehlen Rangkorrelationstests gänzlich.
Für den professionellen Einsatz empfehlen wir daher SPSS, sofern ein zugängliches Interface gewünscht ist, und STATA und R, wenn die algorithmischen Möglichkeiten Priorität genießen.
Robert Grünwald ist Gründer von der Statistik Beratung Novustat und beschäftigt sich schon seit 5 Jahren mit verschiedensten Themen der Statistik.
P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.