Kürzlich hatte ich im Artikel Zählen und addieren mal ganz anders beschrieben, wie man eine Rechenoperation nur auf gerade oder nur auf ungerade Zahlen anwendet.
Das heutige Problem ist ähnlich gelagert: Diesmal soll jedoch nur mit jeder zweiten, dritten oder x-ten Zeile in der Tabelle gerechnet werden.
Auch hier ist die SUMMENPRODUKT-Funktion wieder unser Freund.
Und so geht’s:
Jede zweite Zeile
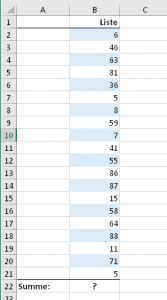
Zur Veranschaulichung habe ich wieder eine kleine Beispieltabelle vorbereitet. Für diese Tabelle soll nun die Summe über jede zweite Zeile, also über die blau markierten Zellen, ermittelt werden:
Beispieltabelle: Jede zweite Zeile addieren
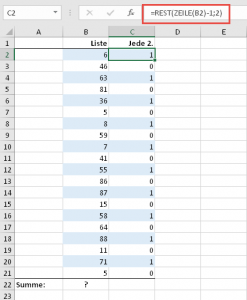
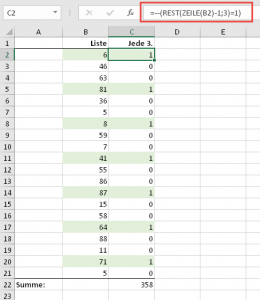
Gehen wir es langsam an und kennzeichnen wir in einer zusätzlichen Spalte mit Hilfe der REST-Funktion jede zweite Zeile:
=REST(ZEILE(B2)-1;2)
Diese Formel zieht von der jeweiligen Zeilennummer den Wert 1 ab, da unsere Tabelle eine Überschrift hat und somit erst in Zeile 2 beginnt. Dann wird dieser Wert durch 2 geteilt. Heraus kommt entweder ein Rest von 1 oder 0:
Hilfsspalte: Mit REST die relevante Zeile bestimmen
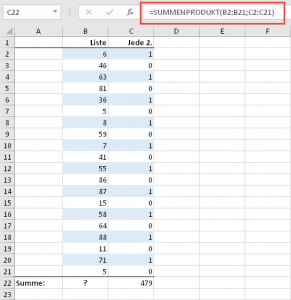
Um für die 1er-Zeilen jetzt die Summe in Spalte B zu bilden, bemühen wir die SUMMENPRODUKT-Funktion. In ihrer einfachsten Form multipliziert sie die Werte aus zwei Spalten und addiert dann die einzelnen Ergebnisse:
=SUMMENPRODUKT(B2:B21;C2:C21)
SUMMENPRODUKT über die Hilfsspalte
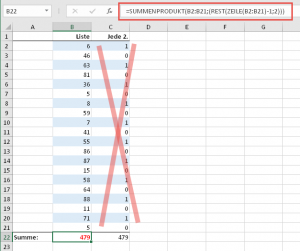
Da wir aber auf die Hilfsspalte gut verzichten können, muss die Formel ein wenig umgebaut werden. Genauer gesagt packen wir jetzt nur die REST-Funktion aus der Hilfsspalte direkt in die SUMMENPRODUKT-Funktion:
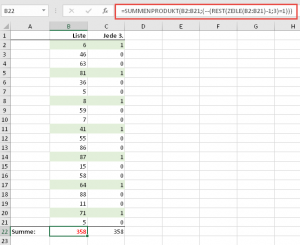
=SUMMENPRODUKT(B2:B21;(REST(ZEILE(B2:B21)-1;2)))
Und schon ist die Hilfsspalte überflüssig:
Alles kompakt in einer Formel
Jede dritte Zeile
Mit einer kleinen Anpassung funktioniert das Ganze auch, wenn jede dritte Zeile addiert werden soll. In der REST-Funktion verwenden wir jetzt als Teiler den Wert 3 und somit kann bei der Division ein Rest von 0, 1 oder 2 herauskommen. Deshalb wird geprüft, ob der Rest = 1 ist. Das Ergebnis dieser Prüfung ist ein Wahrheitswert WAHR oder FALSCH, den wir mit den doppelten Minuszeichen in 1 oder 0 umwandeln:
=--(REST(ZEILE(B2)-1;3)=1)
Die Summe unter Einbeziehung dieser Hilfsspalte wird wieder über SUMMENPRODUKT ermittelt:
=SUMMENPRODUKT(B2:B21;C2:C21)
REST-Funktion für jede dritte Zeile
Aber auch hier wollen wir natürlich wieder auf die Hilfsspalte verzichten und packen die REST-Funktion direkt in die SUMMENPRODUKT-Funktion:
=SUMMENPRODUKT(B2:B21;(--(REST(ZEILE(B2:B21)-1;3)=1)))
Und wieder kombiniert in einer Formel
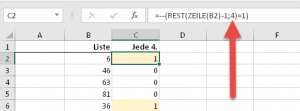
Dieses Spiel kannst Du jetzt bis zur Verblödung weitertreiben: Du musst lediglich den Teiler in der REST-Funktion anpassen:
Der Teiler macht den Unterschied
Zugegeben, das sind keine Anwendungsfälle, über die du jeden Tag stolpern wirst. Aber sie zeigen die Vielseitigkeit der SUMMENPRODUKT-Funktion. Und wer weiß, vielleicht ist das für Dich ja der Beginn einer großen Freundschaft…
P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.
Hallo Martin,
vielen Dank für diesen Beitrag zum Thema Summenprodukt. Ich muss gestehen, die Art wie du die Formel nutz, nutze ich sie nie (Ich nutzte kein „;“ sondern immer nur „*“.
Kannst du mir eventuell sagen,warum du diesen Weg gewählt hast? Ich hätte es so gebaut:
=SUMMENPRODUKT((B2:B21)*(REST(ZEILE(B2:B21)-1;2)=1))
Nicht zuletzt, weil ich recht einfach eine Funktin draus bauen kann, die mir z.B. jede 2. und 4. Zeile addiert und ausgibt.
Würde mich halt interessieren, was die vorteile von dem „;“ in Summenprodukt ist
Viele Grüße
Ruben
Hallo Ruben,
es gibt keinen speziellen Grund, warum ich das Semikolon verwendet habe. Beides hat hier den gleichen Effekt.
Schöne Grüße,
Martin
Das gleiche kann auch über eine Matrixformel gelöst werden:
={SUMME(WENN((REST(ZEILE(B2:B21)-1;2))=0;B2:B21;0))}
={SUMME(WENN((REST(ZEILE(B2:B21)-1;3))=0;B2:B21;0))}
={SUMME(WENN((REST(ZEILE(B2:B21)-1;4))=0;B2:B21;0))}
…
Interessant wäre ein Vergleich der Performance.
Schöne Grüße
Marcel
Das gleiche kann auch mit Summenprodukt gelöst werden:
=SUMMENPRODUKT((B2:B21)*(REST(ZEILE(B2:B21)-1;2)=0))
=SUMMENPRODUKT((B2:B21)*(REST(ZEILE(B2:B21)-1;3)=0))
=SUMMENPRODUKT((B2:B21)*(REST(ZEILE(B2:B21)-1;4)=0))
Schöne Grüße
Marcel
Es gibt einen Unterschied in der Reihenfolge der Ausführung.
So wird bei =SUMMENPRODUKT(Matrix1*Matrix2) erst {Matrix1*Matrix2} gerechnet und anschließend die Vektorsumme berechnet (SUMMENPRODUKT mit einem Argument = Vektorsumme).
=SUMMENPRODUKT(Matrix1;Matrix2) ist jedoch performanter, da der Zwischenweg über einen Hilfsvektor entfällt, somit Speicher gespart wird und zudem effizientere SSE2-Operationen auf dem Prozessor ausgeführt werden können.
Ich meinte natürlich AVX-Befehle, da habe ich wohl etwas durcheinander gebracht …
Hallo Maja,
danke für diese Info. Ich merke schon, da kennt sich jemand ziemlich gut aus…
Schöne Grüße,
Martin
Hallo Martin, ich bin bei einer Excel-Herausforderung („Probleme“ mit Excel kann es ja nicht geben 🙂 ) auf deine Seite gestoßen.
Die Formel für „jede x. Zeile addieren“ bräuchte ich geändert auf „jede x. Zeile multiplizieren“.
Auf dein Beispiel oben gemünzt wäre das:
B2*B3 + B4*B5 + B6*B7 etc
Hast du dazu eine Idee?
Danke schon jetzt, lg, Bernhard
Hallo Bernhard,
ich bin mir nicht sicher, ob sich das so unmittelbar mit einer Formel umsetzen lässt. Ich würde wahrscheinlich versuchen, die zu multiplizierenden Werte in zwei Spalten nebeneinander zu bringen und dann die Multiplikation auszuführen. Also mit Hilfsspalten und Hilfsformeln. Eine elegante Lösung fällt mir spontan jedenfalls nicht ein. Aber vielleicht hat ein ein anderer Leser eine Idee.
Schöne Grüße,
Martin
Schöne Grüße,
Martin
Hallo,
an sich funktioniert die Formel sehr gut nur habe ich das Problem das ich nur jede 13te Zeile Zählen will. Nach langen porbieren ist mir aufgefallen das die Formel nur bis zu einem Teiler von 10 funktioniert. Sobald ich den 11ten, 12ten oder auch 13ten (den ich brauche) eingebe kommt als Ergebnis immer eine „0“.
Warum ist das so? Wo liegt mein Denkfehler?
Hier mal die Formel die ich verwende:
{=SUMME((WENN(REST(ZEILE(O31:O324);13)=1;O31:O324)=V2)*1)}
Danke schonmal im Voraus
Gruß Torsten
Hallo Torsten,
zwei Dinge fallen mir in deiner Formel auf bzw. erschließen sich mir nicht:
– mir ist nicht klar, was =V2 in der Formel bezwecken soll
– da deine Tabelle erst ab Zeile 31 beginnt, musst du den Wert 30 von der ZEILE-Funktion abziehen.
Mein Vorschlag wäre daher:
{=SUMME((WENN(REST(ZEILE(O31:O324)-30;13)=1;O31:O324))*1)}
Schöne Grüße,
Martin
Hallo Martin,
danke für deine Antwort. Ich werde die Formel gleich mal anpassen.
V2 ist die Bedingung, also wenn im Bereich O31:O324 der Inhalt aus der Zelle V2 enthalten ist. Da der Inhalt von dieser Zelle aber in mehreren Zeilen vorkommen kann darf Excel eben nur jede 13te Zeile berücksichtigen;)
Hallo Martin,
nachdem ich den Wert 30 in der ZEILE-Funktion abgezogen hab funktioniert die Formel jetzt genauso wie ich das wollte.
Vielen dank nochmal
Gruß Torsten
Hat mir sehr geholfen.
Danke.
Aber wie finde ich den Maximalwert aus jeder 3. Zelle – und wie den Minimalwert?
Und wie ermittle ich, wie viele Zellen es insgesamt sind (jede 3. Zelle)?
Dank
Hallo Detlef,
die einzige Lösung, die mir spontan einfällt, benötigt die FILTER-Funktion (nur in M365 oder Excel 2021 verfügbar). Bezogen auf das Beispiel von oben wären das dann folgende Formeln:
Minimum: =MIN(FILTER(B2:B21;–REST(ZEILE(B2:B21)-1;3)=1))
Maximum: =MAX(FILTER(B2:B21;–REST(ZEILE(B2:B21)-1;3)=1))
Anzahl: =ANZAHL(FILTER(B2:B21;–REST(ZEILE(B2:B21)-1;3)=1))
Schöne Grüße,
Martin
hm…
ich arbeite mit LibreOffice.
🙁
Im LibreOffice-Forum hab ich Hilfe erhalten:
https://www.libreoffice-forum.de/viewtopic.php?f=6&t=39095&p=104558#p104558
soweit funktoniert das und die Frage ist (eigentlich) gelöst, aber nach jedme „eigentlich“ kommt ein „aber“:
Hier hat Maja Staus am 14.06.2017 um 00:45 geschrieben:
„=SUMMENPRODUKT(Matrix1;Matrix2) ist jedoch performanter, da der Zwischenweg über einen Hilfsvektor entfällt, somit Speicher gespart wird und zudem effizientere SSE2-Operationen auf dem Prozessor ausgeführt werden können.“
Und deshalb hätte mich diese/so eine (schnellere/kleinere/leichtere) Alternative zur Matrix-Berechnung inteessiert.
Anmerkung: Ich gehe mal davon aus, dass das (eigentlich) nur bei Riesentabellen und/oder bei wisenschaftlichen und/oder Großkonzernberechnungen tatsächlich relevant ist… es geht mir dabei eher um Vollständigkeit der Möglichkeiten, denn bekanntlich führen meistens viele Wege nach Bielefeld (um nicht immer alle nach Rom zu schicken).