Manchmal steht man in Excel vor einer Aufgabe und denkt sich: Das ist doch ganze einfach! Aber auf den zweiten Blick stellt man fest: Mist, doch nicht so einfach…
Hast du zum Beispiel schon einmal versucht, nur mit Hilfe von Formeln einen bestimmten Wert in einer Tabelle zu finden? Also eine Suche, die sich sowohl über mehrere Spalten als auch über mehrere Zeilen erstreckt? Klingt eigentlich ganz einfach, oder?
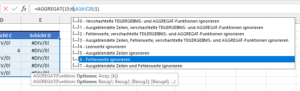
Dann lass dich mal überraschen. Denn die Lösung führt über eine Funktion, die völlig zu Unrecht ein ziemliches Schattendasein fristet: AGGREGAT
Und so geht’s:
Die Aufgabe
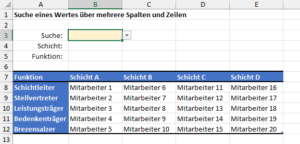
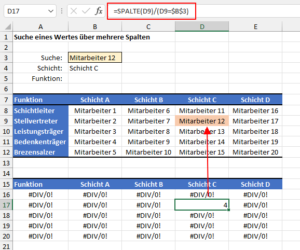
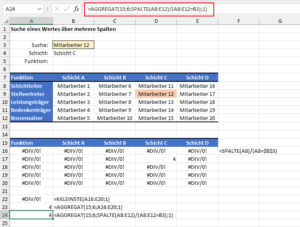
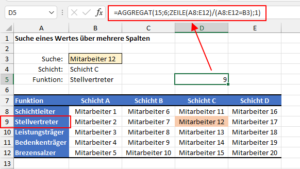
Ich habe einen kleinen Schichtplan, in dem verschiedene Mitarbeiter entsprechend ihrer Funktion und der zugeteilten Schicht eingetragen sind. Die Beispieltabelle kannst du dir hier herunterladen.
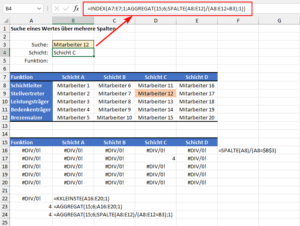
Nun möchte ich in einem Suchfeld einen Mitarbeiter auswählen und mir dann anzeigen lassen, welcher Schicht er zugeordnet ist und welche Funktion er hat:
Finde zu einem Mitarbeiter Schicht und Funktion
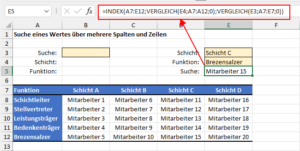
Hieße die Aufgabenstellung beispielsweise: Wer ist der Brezensalzer von Schicht C, wäre eine Lösung mit Hilfe von INDEX und VERGLEICH relative schnell gefunden:
Anders herum wäre es einfach
Unsere Aufgabe ist aber genau anders herum: Wir kennen zwar den Mitarbeiter, aber wir wissen weder die Zeile noch die Spalte, in der er zu finden ist. Nun ist guter Rat teuer…
Lösung Teil 1: Finden der Schicht
Die INDEX-Funktion ist grundsätzlich schon ein sehr guter Ausgangspunkt, liefert sie doch einen Wert zurück, der sich in einer angegebenen Zeile und/oder Spalte befindet:
=INDEX(Matrix;Zeile;Spalte)
Für die Ausgabe der können wir uns auf die Kopfzeile beschränken, bezogen auf mein Beispiel wäre das also
=INDEX(A7:E7;1;Spalte)
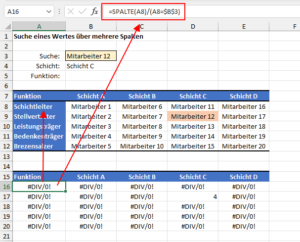
Fehlt also nur noch das Spalten-Argument. Dazu könnten wir die Funktion SPALTE nutzen. Sie soll aber nur dann eine Spaltennummer zurückliefern, wenn der Wert der Zeile auch dem gesuchten Mitarbeiter entspricht. Daher können wir folgende Formel verwenden, die ich zur Verdeutlichung in einer kleinen Hilfstabelle eingetragen habe:
Eine Hilfstabelle sorgt für mehr Transparenz
Für die erste Zelle prüfen wir =SPALTE(A8)/(A8=$B$3)
Für die Zellen daneben sieht es so aus:
=SPALTE(B8)/(B8=$B$3)
=SPALTE(C8)/(C8=$B$3)
und so weiter.
Wenn der Wert der Zelle nicht dem gesuchten Mitarbeiter entspricht, wird der Divisor FALSCH bzw. 0. Daher erhalten wir fast überall den Fehlerwert #DIV/0! Bis auf die einzige Zelle D17, die den Wert 4 für die vierte Spalte liefert:
Der gesuchte Mitarbeiter steht in Spalte 4
Denn hier ist das Ergebnis von (D9=$B$3) WAHR bzw. 1 und damit gibt es eine gültige Division.
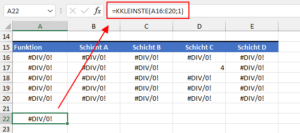
Nun brauchen wir also nur noch den einzigen Wert aus unserer Hilfstabelle – als 4 – der auch gleichzeitig der kleinste Wert in der Tabelle ist. Dafür wäre grundsätzlich die KKLEINSTE-Funktion geeignet, wenn in der Tabelle keine Fehlerwerte enthalten wären. Denn damit kann diese Funktion nicht umgehen und liefert selbst einen Fehler:
KKLEINSTE liefert nur einen Fehler
Und genau an dieser Stelle kommt unsere Geheimwaffe zum Einsatz: Die AGGREGAT-Funktion.
Lösung Teil 1
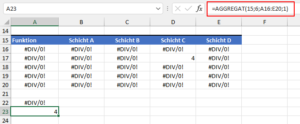
Wie schon in diesem Artikel beschrieben, ist AGGREGAT ein echtes Multitalent, das viele Funktionen in sich vereinigt. Neunzehn Stück, um genau zu sein. Und dazu gehört auch die KKLEINSTE-Funktion. Wenn wir AGGREGAT jetzt auf unsere Hilfstabelle loslassen, kommt der gewünschte Wert 4 heraus:
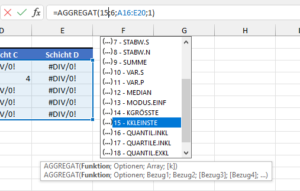
=AGGREGAT(15;6;A16:E20;1)
AGGREGAT liefert das Ergebnis
Die Nummer 15 im ersten Argument steht für die KKLEINSTE-Funktion:
Funktion 15 = KKLEINSTE
Das zweite Argument in der Formel sorgt dafür, dass Fehlerwerte ignoriert werden:
Option 6 ignoriert Fehlerwerte
Und da wir natürlich auf unsere Hilfstabelle verzichten wollen, packen wir die entsprechende Formel aus der Hilfstabelle noch gleich in die AGGREGAT-Funktion. Das Schöne dabei ist, dass man nicht nur eine einzelne Zelle ansprechen kann, sondern den gesamten Bereich:
AGGREGAT klappt auch ohne Hilfstabelle
=AGGREGAT(15;6;SPALTE(A8:E12)/(A8:E12=B3);1)
Jetzt haben wir alles, um in Kombination mit der Index-Funktion auf die richtige Spalte 4 zugreifen zu können und somit für den Mitarbeiter 12 als Ergebnis die Schicht C erhalten:
Die komplette Formel für die Schicht
Lösung Teil 2
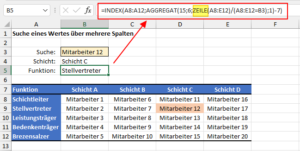
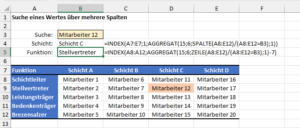
Jetzt wo wir die Schicht kennen, wollen wir noch die Funktion des Mitarbeiters bestimmen. Auch dafür greifen wir auf die Kombination aus INDEX und AGGREGAT zurück, nur dass wir jetzt eben nicht die erste Zeile der Tabelle, sondern die erste Spalte durchsuchen.
Folglich ersetzen wir die SPALTE-Funktion durch die ZEILE-Funktion:
Die komplette Formel für die Funktion
Aber warum ziehe ich am Ende der Formel den Wert 7 ab? Ohne diese Subtraktion würde die AGGREGAT-Funktion für den Mitarbeiter 12 die Zeile 9 zurückliefern, was grundsätzlich richtig ist.
Ohne Subtraktion wird die absolute Zeilennummer geliefert
Für die INDEX-Funktion brauchen wir aber nicht die absolute Zeilennummer, sondern die relative Zeile innerhalb unserer Schichttabelle. Da unsere erst Tabelle in Zeile 7 beginnt, muss ich den Wert 7 wieder abziehen, um auf die richtige Zeilennummer zu kommen. Hier nochmal die beiden Formeln im direkten Vergleich:
Beide Formeln im direkten Vergleich
Ich gebe zu, die Lösung war etwas kniffelig. Wenn man sich aber mal eine Weile damit beschäftigt hat, wird sie sicherlich nach und nach besser verständlich. Und sie zeigt, wie mächtig die vernachlässigte AGGREGAT-Funktion eigentlich ist.
Hättest du diese Aufgabe anders gelöst? Wenn ja, lass es uns in den Kommentaren wissen!
P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.
Hallo Martin,
ich habe ein Problem und hoffe, du kannst mir helfen 🙂
In einer Tabelle habe ich Artikelnummern, die teilweise mehrfach vorkommen. Ich möchte nun wissen, wann die jeweilige Artikelnummer zum ersten Mal erscheint (da könnte dann z.B. in der Spalte daneben eine „1“ stehen). Das bekomme ich leicht mit ZÄHLENWENNS hin. Meine Tabelle kann aber gefiltert werden, und die „1“ soll dann bei der jeweiligen ersten SICHTBAREN Artikelnummer stehen. Könnte vielleicht mit einer Kombination aus AGGREGAT und ZÄHLENWENNS funktionieren, hast du eine Idee? (Also feststellen des jeweiligen ersten Vorkommens in nur sichtbaren Zellen)
Vielen herzlichen Dank!!!!
LG
Alex
Hallo Martin,
In Teil 2 könnte man statt der fixen minus sieben wieder die Zeilen-Funktion verwenden (ZEILE(7:7)). Dann funktioniert die Lösung auch noch, wenn weitere Zeilen eingefügt werden.
SG
Marcel
Hallo Marcel,
stimmt, danke für diese hilfreiche Ergänzung!
Schöne Grüße,
Martin
Inzwischen habe ich selbst eine Lösung gefunden. Es mag nicht die eleganteste Lösung sein, aber sie funktioniert. Da diese aber mit dem Thema wenig zu tun hat, entschuldige ich mich für den Fehlbeitrag. In der Formel ist zu beachten, dass sich die Zellbezüge etwas verschoben haben, aber der Aufbau gleich blieb.
=SUMME(SUMMENPRODUKT(
(WENN($D$10:$D$40″“;$D$10:$D$40;0))*
(N($C$10:$C$40=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($F$10:$F$40<=F10)));
SUMMENPRODUKT(
(WENN($N$10:$N$40″“;$N$10:$N$40;0))*
(N($M$10:$M$40=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($P$10:$P$40<=F10)));
SUMMENPRODUKT(
(WENN($X$10:$X$40″“;$X$10:$X$40;0))*
(N($W$10:$W$40=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($Z$10:$Z$40<=F10)));
SUMMENPRODUKT(
(WENN($AH$10:$AH$40″“;$AH$10:$AH$40;0))*
(N($AG$10:$AG$40=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($AJ$10:$AJ$40<=F10)));
SUMMENPRODUKT(
(WENN($AR$10:$AR$40″“;$AR$10:$AR$40;0))*
(N($AQ$10:$AQ$40=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($AT$10:$AT$40<=F10)));
SUMMENPRODUKT(
(WENN($BB$10:$BB$40″“;$BB$10:$BB$40;0))*
(N($BA$10:$BA$40=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($BD$10:$BD$40<=F10)));
SUMMENPRODUKT(
(WENN($D$46:$D$76″“;$D$46:$D$76;0))*
(N($C$46:$C$76=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($F$46:$F$76<=F10)));
SUMMENPRODUKT(
(WENN($N$46:$N$76″“;$N$46:$N$76;0))*
(N($M$46:$M$76=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($P$46:$P$76<=F10)));
SUMMENPRODUKT(
(WENN($X$46:$X$76″“;$X$46:$X$76;0))*
(N($W$46:$W$76=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($X$46:$X$76<=F10)));
SUMMENPRODUKT(
(WENN($AH$46:$AH$76″“;$AH$46:$AH$76;0))*
(N($AG$46:$AG$76=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($AJ$46:$AJ$76<=F10)));
SUMMENPRODUKT(
(WENN($AR$46:$AR$76″“;$AR$46:$AR$76;0))*
(N($AQ$46:$AQ$76=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($AT$46:$AT$76<=F10)));
SUMMENPRODUKT(
(WENN($BB$46:$BB$76″“;$BB$46:$BB$76;0))*
(N($BA$46:$BA$76=WENN(GANZZAHL((F10-$H$5)/63)+1<1;GANZZAHL((F10-$H$5)/63);GANZZAHL((F10-$H$5)/63)+1)))*
(N($BD$46:$BD$76<=F10))))
Hallo Roger,
freut mich zu hören, dass du eine Lösung gefunden hast. Auch wenn dieses Formelmonster für Aussenstehende nicht nachvollziehbar ist 😉
Macht aber nichts. Wichtig ist, dass es für dich funktioniert!
Schöne Grüße,
Martin
Hallo Martin,
das hast du sehr diplomatisch kommentiert. Ich bin heute nach einiger Zeit wieder auf diese Seite gestoßen und mußte über meine eigene Formel schmunzeln. Mittlerweile konnte ich die Formel u.a. mit Let- & Stapel-Funktion auf mindestens ein zwanzigstel kürzen. Dennoch war bereits der 1. Beitrag am Thema vorbei, daher kannst du auch diesen und den vorherigen Beitrag von mir löschen, wenn es dir möglich ist.
Gruß
Roger