Nachdem wir in den beiden letzten Teilen gesehen haben, wie man die Höhe von Ratenzahlungen oder das benötigte Start- oder Zielkapital berechnen kann, geht es diesmal um die Laufzeit.
Mit der heutigen Excel-Funktion können wir endlich berechnen, wie lange etwas dauert. Zum Beispiel
- bis ein Kredit zurückbezahlt ist
- bis ein bestimmtes Sparziel erreicht ist
- bis ein vorhandenes Vermögen verbraucht ist
Die Antworten auf diese und ähnliche Fragen liefert die ZZR-Funktion (ZZR = Zahlungszeiträume). Und so geht’s:
Die ZZR-Funktion
Bevor wir uns der Praxis zuwenden, gibt es erst mal wieder ein wenig Excel-Theorie:
Die ZZR-Funktion berechnet die Anzahl der Zahlungszeiträume, die für eine bestimmte Investition erforderlich sind. Mit anderen Worten: Wie lange dauert es, bis ein bestimmtes Ziel erreicht ist. Das kann die z.B. Tilgung eines Kredits oder das Ansparen eines Sparvertrags sein.
Dabei werden regelmäßige Zahlungen gleicher Höhe zugrunde gelegt und der Zinseszins-Effekt berücksichtigt; möglich sind aber auch etwaige Einmalzahlungen zu Beginn oder am Ende der Laufzeit.
Die allgemeine Syntax sieht wie folgt aus:
=ZZR(Zins; Rmz; BW; [Zw]; [F])
Zins:
Das ist der Zinssatz pro Periode bzw. Zahlungszeitraum. Da Zinssätze üblicherweise für 1 Jahr angegeben werden, muss bei monatlichen Zahlungen der Zinssatz durch 12, bei vierteljährlichen Zahlungen durch 4 usw. geteilt werden.
Rmz:
ist der konstante Betrag, der in jeder Periode bezahlt wird (Rmz = Regelmäßige Zahlungen). Man spricht hier auch von einer Annuität. Im Falle eines Darlehens setzt sie sich zusammen aus dem Zinsanteil und dem Tilgungsanteil.
BW:
Der Barwert ist der Anfangsbestand zu Beginn der Zahlungen. Im Falle eines Kredits wäre das also die Kreditsumme, im Falle von Rentenauszahlungen das Anfangskapital, das zu Beginn zur Verfügung steht.
Zw:
Der zukünftige Wert ist der Endwert, den man nach der letzten Zahlung erreicht hat. Dieser Parameter ist optional, kann also auch weggelassen werden. Der angenommene Endwert ist dann Null. Hier könnte aber z.B. auch der Restwert stehen, den man am Ende seiner Tilgungsraten erreicht haben möchte.
F:
Damit gibt man die Fälligkeit an: 1 bedeutet, die Zahlung ist zu Beginn der Periode fällig, 0 (Null, oder nicht angegeben) bedeutet, die Zahlung ist am Ende der Periode fällig.
Schauen wir uns wieder ein paar praktische Anwendungsfälle an.
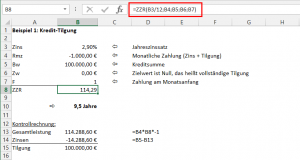
Beispiel 1: Kredit-Tilgung
Wir haben uns für den Hausbau einen Kredit von 100.000,- Euro aufgenommen. Wie lange dauert es, bis er bei einem Jahreszinssatz von 2,9 % vollständig zurückbezahlt ist, wenn wir monatlich 1.000,- Euro abbezahlen können (Zins + Tilgung)?
Aufpassen:
Da es sich bei den 2,9 % um einen Jahreszins handelt, wir aber monatliche Raten bezahlen, müssen wir den Zinssatz in unserer Formel durch 12 teilen. Die Zahlungsperiode und die Zinsperiode müssen immer übereinstimmen.
Wir müssten also unseren 100.000-Euro-Kredit gut 114 Monate lang abstottern, dass entspricht etwa 9,5 Jahre. Wie man an der Kontrollrechnung sieht, belaufen sich unsere Zahlungen inklusive Zinsen dabei auf insgesamt 114.288 Euro.
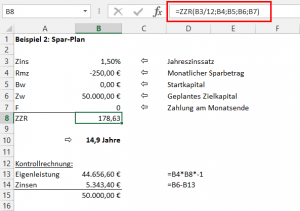
Beispiel 2: Sparplan
Eine andere Fragestellung, die mit der ZZR-Funktion zu lösen ist: Wie lange dauert es, bis ich ein bestimmtes Vermögen angespart habe?
Im folgenden Beispiel wollen wir jeweils am Ende des Monats 250,- Euro auf die hohe Kante legen und gehen von einer sagenhaften Verzinsung von 1,5 % p.a. (per annum / pro Jahr) aus. Unser Sparziel liegt bei 50.000,- Euro. Wie lange müssen wir sparen?
Die ZZR-Funktion bringt die etwas frustrierende Erkenntnis ans Tageslicht: Wir müssen fast 15 Jahre lang sparen, um auf die gewünschten 50.000,- Euro zu kommen. Der Zinsertrag läge bei 5.343 Euro, die Eigenleistung bei gut 44.656 Euro. Also das Geld doch besser gleich auf den Kopf hauen…
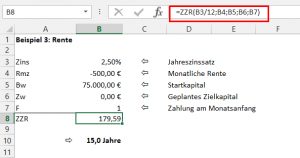
Beispiel 3: Rente
Unser reicher Onkel in Amerika hinterlässt uns ein Erbe von umgerechnet 75.000,- Euro. Davon möchten wir unser Gehalt oder unsere Rente monatlich um 500,- Euro aufbessern. Wie lange reicht das Erbe, wenn wir eine Verzinsung von 2,5 % unterstellen?
Wie man sieht, könnten wir ziemlich genau 15 Jahre lang mit zusätzlichen 500,- Euro pro Monat rechnen, bis das Erbe komplett aufgebraucht ist. Jetzt müsste sich nur noch der Onkel dazu finden…
So, das war jetzt der dritte und letzte Teil meines Ausflugs in die Welt der finanzmathematischen Excel-Funktionen. Excel bietet hier noch eine Unmenge weiterer Funktionen an, mit denen ich Dich vielleicht irgendwann einmal quälen werde.
Zum Schluß noch ein Blick über den Tellerrand hinaus:
Gerhard Pundt hat auf seinem Blog ebenfalls einen interessanten Artikel zu diesem Thema veröffentlicht:
Sparen mit Excel und finanzmathematischen Funktionen
Und dann reicht es aber vorläufig wieder mit der Finanzmathematik, würde ich sagen. Oder?

P.S. Die Lösung ist immer einfach. Man muss sie nur finden.
(Alexander Solschenizyn)
P.P.S. Das Problem sitzt meistens vor dem Computer.